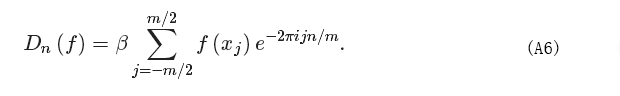如特安防
您只需一个电话我们竭诚为您服务
- 全国统一服务热线
- 18668913066
相关资讯

咨询热线:
18668913066
固话:0531-58615066
邮箱:2881529222@qq.com
地址:山东省济南市历下区华阳路高校商务港1号楼
如特安防手机版网站二维码
当前位置:
新奇的半参数算法,用于免干扰调谐吸收光谱气体传感
摘要
气体传感性能最普通的限制之一,是出现意想不到的干涉条纹,例如,光路中表面之间多次反射。还有, 这些干扰的振幅和频率依赖于光学元件距离和调准,并受温度变化和机械扰动的影响,产生信号漂移。现在,我们提出一个新奇半参数算法,从含有随意干扰的背景中(没有就这些干扰的函数形式作出任何假设), 算法允许信号提取,像一个气体分子的光谱吸收线。算法首先应用到模拟数据,接着在强干扰条纹中进行氧气吸收测量。就作者所知,如果干涉条纹有一个自由光谱限度,有比得上那些被检测信号的振幅,那么算法特别使前所未有的准确性成为可能的。描述的方法显现出纯粹基于后处理的优势。如果知道信号傅里叶变换函数形式,描述的方法是极其直接的实现。所以,它有潜力使免干扰吸收光谱成为可能的。最后, 它的实用性越过气体传感吸收光谱,因为它可应用到任何类型的光谱数据。
关键词:干扰,干扰消除,噪声降低,数字滤波,光谱学,传感器
1.介绍
归功于激光源和光电元件的可利用性和性能的巨大进步, 可调谐二极管激光吸收光谱(TDLAS)已参入研究和工业应用的各种学科。作为高敏感性、可选择性、快捷的、无损的,和原位法, TDLAS在目前越来越多的用在几个领域来定量评估气体浓度。这些领域包括,仅仅提及几个,大气环境监测[1,2,3,4,5,6],医学诊断[7,8,9],化学分析[10],和工来加工控制[11,12,13]。应用量的增加,已推动在敏感性和稳定性上对这种方法的需求。在另一方面,对实践和经济运用,有正日益增长的兴趣:紧凑、设计简单、成本低的敏感性传感器,不要求特别的光元件,但保证实现复杂实验室设备的敏感性。
传感器性能最普通的限制之一,是标准具出现意想不到的干涉条纹[14]。这些干扰可能起自系统中的多次反射和散射面,像反光镜、透镜、光纤端面、激光头窗口或气体中的尘粒[14]。甚至散布性的表面,如,因传感器窗口积尘,随时产生干扰条纹。特别地,条纹有与吸收线宽相似的自由光谱区(FSR),在线性特征的测定上促成重大错误。特别的策略已提出来解决这些类型的干扰,例如,参考[16]中,小的干扰条纹振幅和一个多样性条纹FSR测量窗口,条纹在傅立叶域分析后,被除去。进一步,因为干扰的振幅和频率依赖于光学元件距离和调准,它们受温度变化和机械扰动的影响,产生,如,信号输出漂移,因而系统的长期性能恶化。
最简单的策略来减小干扰条纹的影响,包括防反射涂层和楔,或光表面角化。别的办法包括,仅提几种:抖动产生干扰的一个表面,整合信号均化影响[18,19],选择一个特别调频[20]或调制方案[21,22],特别地选择干扰表面的距离[23],和后处理滤波[24]。关于单一增强和噪声去除技术的综合评述,见参考[25]。虽然,所有这些方法在过去的几年里已成功地运用,但是它们在实际应用上有限制,在依赖于特别应用条件的实施上有限制。例如,不可能总抖动一个表面,一个特别检测方案的运用可能受限于测量的灵活性上。
本工作,提出一种新的和广泛使用的方法,仅依靠数据的后处理。因此,不要求设备设置或硬件的调整,并容易地适用于不同实验配置。这新出的算法允许信号提取,像一个气体分子的吸收线信号。就那些干扰特点的函数方式没有做任何假定,从含有任意干扰的背景中提取信号。因此,有改进TDLAS敏感性和稳定性的潜力。进一步地,本算法,特别易于应用。如果信号的傅里叶变换能以封闭形式写出,本算法能非常普遍地用于任何类的光谱数据。本论文组织如下:第2节,描述方法和算法的基础;第3节,论证它在模似信号方面的应用;第4节,说明直接吸收光谱用于氧气气体传感的一个实例结果。
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
本工作,提出一种新的和广泛使用的方法,仅依靠数据的后处理。因此,不要求设备设置或硬件的调整,并容易地适用于不同实验配置。这新出的算法允许信号提取,像一个气体分子的吸收线信号。就那些干扰特点的函数方式没有做任何假定,从含有任意干扰的背景中提取信号。因此,有改进TDLAS敏感性和稳定性的潜力。进一步地,本算法,特别易于应用。如果信号的傅里叶变换能以封闭形式写出,本算法能非常普遍地用于任何类的光谱数据。本论文组织如下:第2节,描述方法和算法的基础;第3节,论证它在模似信号方面的应用;第4节,说明直接吸收光谱用于氧气气体传感的一个实例结果。
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
2.算法描述
本工作中,算法有能力从不需要模型化的任意背景中,签别一个光谱特征。实验中检测的总信号,这里指“总信号” Itot(x),被模型化为两方面之和:一是光谱特征,像一条吸收线,这里说成“信号”I(x);一是背景,这里说成“背景”B(x):
Itot(x) = I(x) + B(x). (1)
就直接吸收光谱来说,I(x)是吸收的,Itot(x)是被 B(x)干扰的吸收。如上所提,如果背景不能由一个公知的分析表达式模型化,方法表现突出。事实上,如果B(x)未知,没有就B(x)函数形式做出假定,不可能完成一个非线性拟合Itot(x),不可能提取信号I(x)。另一方面,如果函数形式已知,但很复杂,本算法可能有优势,因为在非线性拟合中背景包含是不可能的。提出的算法另一重要的优势是提取工作完美地独立于干扰振幅之外,如第3节、第4节所陈述。
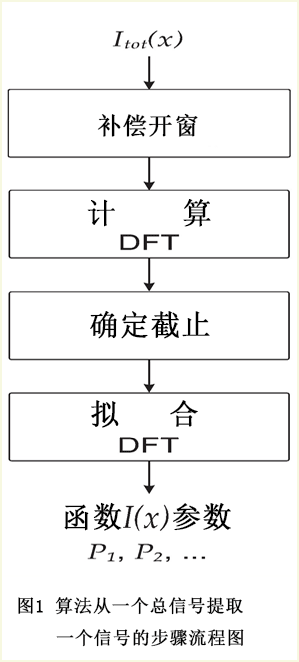
2.1算法的步骤:总述
在说明算法步骤之前,介绍系统命名法和假设。算法是基于主要假设: 背景B(x)的傅里叶变换是明显的不同于0,仅k的一些取值比某一截止点k0小。
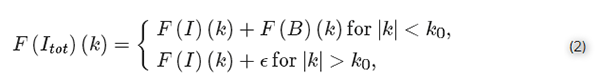
上方程中, F( • )表示连续傅里叶变换(CFT),k0是一个截止频率,ϵ 含F(B)(k)因|k| > k0的分摊额,分摊额是无足轻重的。一个中心方面是,决定截止频率一个合理估值,如“确定截止”节中所述。
注意,本公式适用连续函数。因为在实践中,将总是仅有离散集点,必须接近方程(2)中的CFT,通过一个可调的离散傅里叶变换(DFT)。
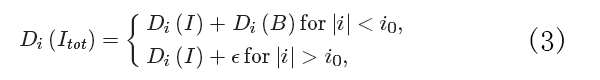
方程(3)中,Di( • )表示可调整的DFT,定义在Appendix A方程式(A6)中, i0:与截频 k0对应的截止点,ϵ 含 Di(B) 因 |i| > i0的分摊额,分摊额被假定成无足轻重的。
图1显示的算法流程图给出直观明白的算法理念。单一步骤的细节如下。
2.2 补偿开窗
在所有实验中,数据总是覆盖一个x方向有限的区。例如,本文中显示的数据是测量一个有限的激光波长范围得到的。数学上,这是等同于在计算傅里叶变换前运用一个矩形窗口(RW)。这个问题在于,如果没有解决,将限制由描述的算法得到的精度。事实上,RW导致方程式2中的ϵ 不再微不足道的,因而致使|F(I(x))(k)|拟合过程出错。这归于一个RW的DFT有一个与1/k成比例的振幅包络线,所以它不再足够快速地转为0。
为减小非常地开窗影响,提出的算法应用到一个更智能的窗口。不经常用的塔基窗口[27,28]有显著的属性,助于极端地戏剧性地减小 ϵ 。塔基窗口,用T(x)表示,完美平坦(常数)中间对称函数,两边快速减至0。
智能地选择塔基函数常量部分的宽度。图2显示一个带有半幅度半宽值(HWHM)的 Lorentzian函数表示为 P2,塔基函数中一个宽度表示为 W,为清晰起见两个函数正常化到1。本工作,a.u. 表示任意单位。从图2中易明白,如果W 比P2明显更大, T(x)I(x) 近似于 I(x)。所以,定义I˜tot(x)=T(x)Itot(x),如下:
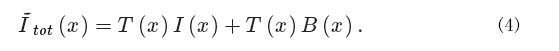
函数中DFT必须计算,取代简单使用 Itot(x)。假定W 比P2 明显更大,方程式(4)近似方程(5)。
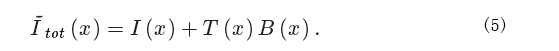
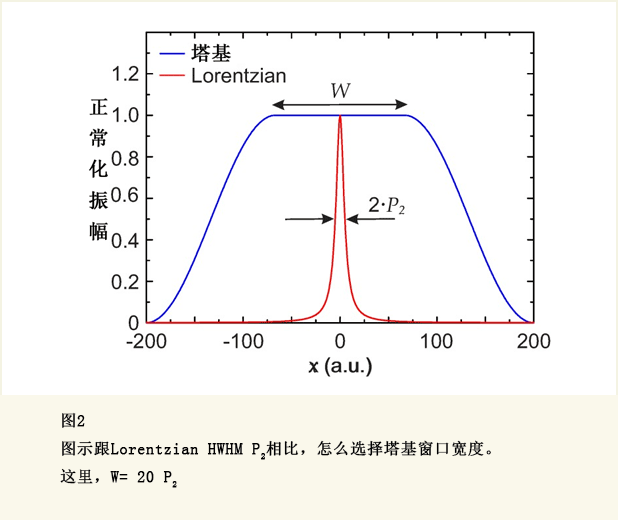
I˜tot(x)是 I(x)信号与背景的总和,背景是原始背景B(x) 和 T(x)的产物,T(x)B(x)。 调整的背景T(x)B(x)有一个傅里叶变换(非常快速地变为0)([27,28])。这意谓着 ϵ 很小,如果考虑 I˜tot(x)取代 Itot(x)。用别的话来说,当使用I˜tot(x)时,ϵ 将包含 Di(T • B)的影响,与比 Di(B)乘以一个RW的值相比,相当小。
在算法的输出和信号 I(x)输入之间,用模拟数据分析绝对偏差,算法效果很好,如是塔基窗口宽度 W ≳ 20 P2。本实验工作中,W = 20 P2用于模拟的和实验得到的数据。W = 20 P2在图2中显示出来。
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
2.3 计算DFT
窗口补偿后的步骤,是计算DFT。能够直接从DFT提取 I(x)参数,由按 Appendix A调整的DFT来近似CFT是必要的。本文展现的所有数据,DFT使用公式(A6)计算。
2.4 确定截止
如图1所示,下一步是确定最佳的截止点i0 ,截止点起一个重要的作用,需要小心选择。本工作提出的方法是选择i0, 以便最大化R2 测定系数,R2是通过拟合DFT使线型傅里叶变换的函数形式的i > i0 后得到的。DFT由方程(7)拟合,后面有较详细的解释。一个运用例子被描述在用pseudo代码写的随后算法中,N指数据集点的数目(即,实验点有限数),D_i 是信号I˜tot(x)的DFT的第i个点。拟合度Rsquared是R2测定的系数,FFFT指I(x)的傅里叶变换函数形式, Rlimity指R2应达到的值。这受限的值是有帮助的,因为,超出某个值,即使提高i0时,R2继续增加,拟合的质量不会显著地改进,且没有必要为了拟合从DFT排除更多的点:
pointtoremove = 0
Rsqmin = 0
for i = 0 to N/2
remove the first i points starting from D_0 to D_{i-1} from the DFT
fit the remaining points D_i to D_{N/2} to the FFFT and save
the fit parameter Rsquared
if (i = 0) then pointtoremove = 0
else if (Rsquared > Rsqmin) then pointtoremove = i and Rsqmin = Rsquared
if (Rsqmin > Rlimit) then break loop
end of for loop.
在上面pseudo代码循环尾部, i0 被确定,保存在变量pointtoremove中。Rsquared可依赖于应用来选择。对于显示在本文中的曲线,循环因Rlimit = 0.99999终止。一个 R2 随 i0 增长进化的例子显示在图3中。涉及第3节后面描述的第3种情况的数据。在 i0 = 30以前, R2还继续轻微增长,但拟合的统计优度不再改进。
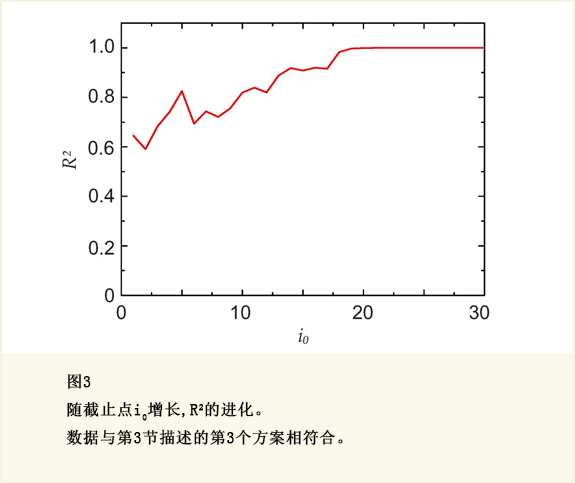
2.5 DFT拟合
算法的最后一步是为了 i > i0执行DFT一个非线性拟合。因为知悉DFT的函数形式,这是一个能被执行的标准处理过程,例如,最小二乘法拟合程序,将不在这里讨论。无需逆向的傅里叶变换,fit I(x) 就被确定,因为|F(I(x))(k)|的函数形式被熟知。
2.6 应用于Lorentzian线形的算法
本节中,Lorentzian信号 I(x)算法的实现,描述为一个例子。这个函数形式被选择,因为它描述许多气体分子的吸收线,如,大气条件下的氧气。在别的条件下,像高温或低压,归因于多普勒增宽的高斯影响不能被被忽视的,且一个佛克脱曲线是最好的描述。Lorentzian函数可写成:

P1, P2 > 0。这在个表达式中,P1 和 P2代表面积和线的HWHM。I(x)特别的有用,因为在直接吸收光谱中,气体浓度可被直接从线下面积测定,因而直接与P1成正比。在这个公式中,|F(I(x))(k)| 是一个简单的指数。

因此,一旦,参数 P1和 P2 从DFT拟合中确定下来,I(x)就知道了。
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
3. 运用模拟数据
新奇的算法首先应用到人为地模拟数据上,来演示它的功能和性能。因为 I(x)信号被提取,可估测算法在不同特征的背景下的精度和稳定性。特别地,带有不同类型定期干扰的三个情形被模拟。信号可被提取,I(x),用于三个情形下同样的Lorentzian函数,Lorentzian函数用方程式(6)的形式写出来( P1 = 5π, P2 = 5)。选择三个情形,反映典型TDLAS的真实情况。
第一个情形,选来表达实验情境,其背景有FSR定期干扰,FSR与被检测的线宽相配。这种背景类型特别地成问题的,因为它强烈影响线形确定。进一步,没有引入一个显著的线形扭曲,它不能由引入二极管激光电流与平均输出的一个小抖动,来去除,或用标准后处理方式来滤除。这种背景被当做一个简单的余弦函数。

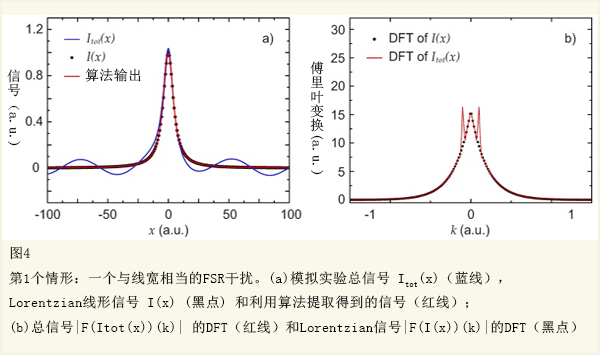
为更好地图示背景的影响, Lorentzian的DFT和总信号的DFTB也显示在图4b中。图中看到的两个峰值表示背景的影响。因有2.1节中的pseudo代码的算法,截止点i0 = 13。
这里讨论的第2个情形,是有以FSR为特征的弱干扰背景,比线宽更大,跟测量范围一样或更大。这种干扰产生于反射——由很短的物理尺寸分隔的两表面之间的反射, 像激光芯片输出面和激光封装的玻璃窗口。选择的函数形式,模拟这种情形如下:

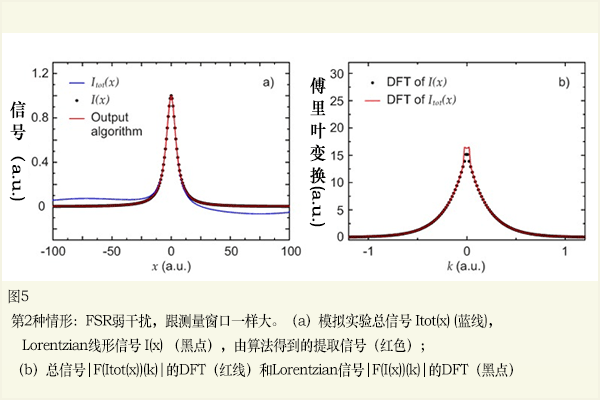
至于第3种情形,考虑一百个余弦函数产生的背景。较少的现实情况是选择论证:无论干扰多么戏剧性,算法可以很好地提出信号I(x)。另外,这种情形图示:背景的函数形式太复杂,不能包括在 Itot(x)的一个非线性拟合中 。背景函数因此写成如下:
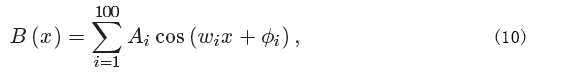
图6a显示总信号 Itot(x),预期的信号I(x),以及运用所描述的算法得到的结果。除了非常复杂的背景,算法能很好地提取信号I(x)。图6b中, 显示Lorentzian的DFT和总信号的DFT。由于背景中有大量余弦函数,DFT有一很结构化的形状。因有2.1节中描述的 pseudo代码算法,截止点 i0 = 30 (也参看图3)。
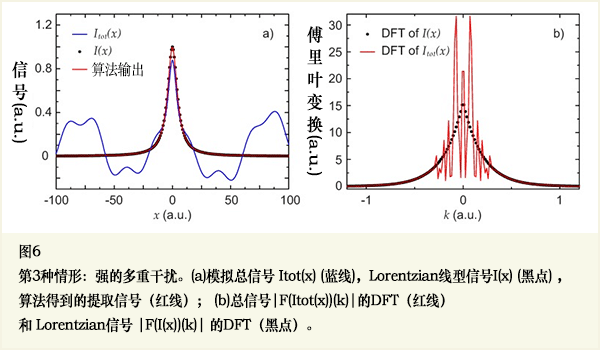
这种情形通过算法得到的描述Lorentzian两参数的百分偏差:P1 为0.012%, P2为0.14%。这种情形下,两参数的偏差特别低。要更好估算两参数的错误和标准偏差,方法是应用到500个函数,这500个函数是利用上面提到的100个余弦函数随机和的产生的函数。接着,错误估出来,研究错误分布。结果,P1 有一个百分误差绝对值的平均值0.12%,其标准偏差0.19%,P2 的是百分误差的平均值0.04%,标准偏差0.06%。
算法提取的参数和启动函数 I(x)的参数之间的不符合,模拟数据算法分析已就这种不符合找原因。主要影响来源于DFT的CFT的近似值,还有一个相当大的点间距,和用在模拟数据的 I(x)的x-区。小的影响源于一个不完善窗口补偿,和一个非常小的频率折叠[30],这里被忽视。因为本文目的是图形化算法,不是最小化差异,模拟数据被选择,尽可能地接近典型实验数据。3种情形算法的应用,已顺利地演示出,即使有像第3种情形非常复杂的背景,我们提出的算法能特别好地提取基础信号。
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
4.实验结果
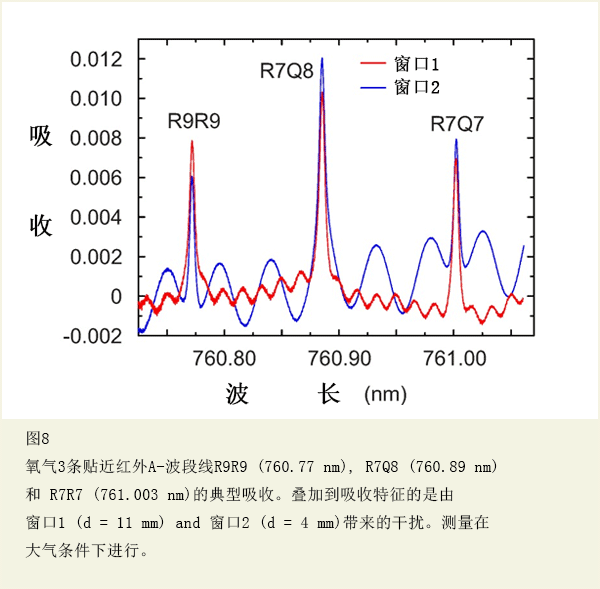
在真实气体传感测量的基础上论证方法的稳定性,在出现多重干涉条纹的情况下,在接近红外A波段的3根氧气强线上做吸收光谱。3根氧气强线:R9R9 (760.77 nm), R7Q8 (760.89 nm)和R7R7 (761.00 nm)。
4.1 实验设置
吸收光谱实验的设置极简单,显示在图7中。
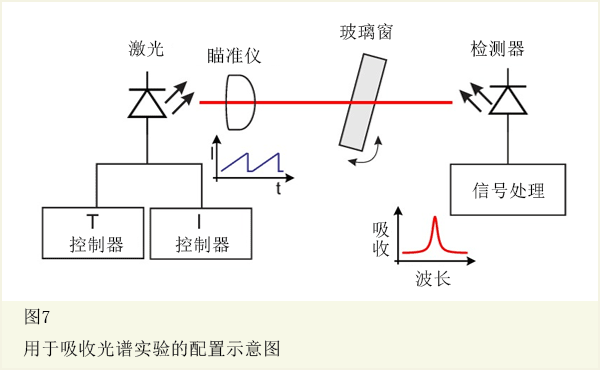
光源是0.25 mW简单模式垂直腔面发射半导体激光器(VCSEL)以760 nm发射(760 nm TO5 VCSEL, Philips Photonics, Ulm, Germany)。激光电流和温度,由一个温度控制器和一个VCSEL激光二极管控制器来调整(温度控制器:LDC 200C, Thorlabs, Newton, NJ, USA;VCSEL激光二极管控制器:LDC 200C, Thorlabs, Newton, NJ, USA)。由透镜校准的激光器进行光发射。样品透射的光,由使用一块大面积硅片10 × 10 mm2 光敏二极管(FS1010, Thorlabs, Newton, NJ, USA)来汇集,由可调收益的光敏二极管放大器(PDA200C, Thorlabs, Newton, NJ, USA)进行放大。使用LabviewTM 软件,DAQ卡(USB-6361, National Instruments Switzerland GmbH, Ennetbaden, Switzerland)的利用电流匝道进行波长扫描和数据采集。选用激光电流扫描来测量3种氧气吸收线。在激光器和探测器之间的总距离,保持固定,大约是36cm。可调强度的干涉条纹通过在光路中插入和倾斜一个已知材料的玻璃窗口来产生。通过改变玻璃窗口的厚度,可实现不同FSR的条纹;通过倾斜玻璃窗口,可调条纹振幅。本工作中,使用两个BK7玻璃窗口(窗口1,厚度11mm;窗口2,厚度为4mm)。这两个窗口来利用比得上窗口1并强于窗口2的信号线宽,创建FSR干扰条纹。这些干扰是最大的干扰,因为它们不易于消除——例如,由激光电流中一个小的振动或标准后处理过滤产生的干扰。
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
4.2 氧气感应
3种氧气的吸收信号线:R9R9, R7Q8 和 R7R7显示在图8中。归因于玻璃窗口的干扰条纹清晰可见。叠加到这些条纹,别的镜像也可见,归因于激光包装的玻璃窗口,以及的瞄准仪表面。零吸收基线源自激光非线性波长依赖强度,由在整个扫描范围之上的一个四阶多项式拟合来测量。本工作报告的所有测量是在空气中做的,在室温和大气压力下。
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
5. 结论
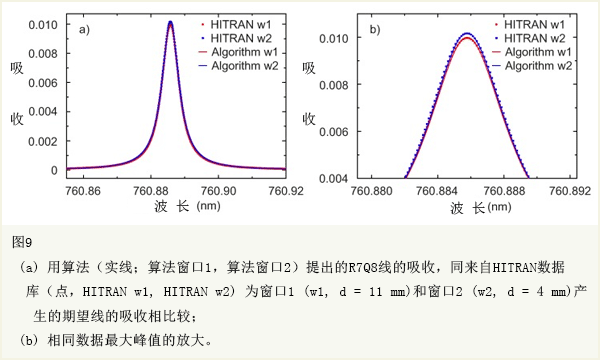
本研究工作中,提出新奇的半参数算法,允许从任意背景中提取信号。特别的,算法应用到不同振幅和FSR的定期干扰条纹汇总的背景中。这些干扰类型,源自,例如,光路中表面之间的多重反射,与吸收光谱有高的相关性,因为它们经常是对气体传感性能最普通的限制。新奇的算法首先在模拟数据上论证。模拟数据,即,代表特别相关实际情况的3种情形的模拟。3种情形中,由算法得到的结果和由线性参数预期值之间不符合度非常小——小于0.3%。接着,算法应用到多重干扰的情况下氧气吸收的实验数据。不管这些强干扰条纹,提取线跟来自HITRAN数据库预期曲线有了显著的的一致性,偏差仅为0.1%。
算法最大的优势是它的半参数。意思是它提取信号,不要求输入参数。这由带有模拟数据的第3种情形明确地论证了,第3种情形背景包括一百个带有不同振幅的余弦函数,频率和相位不能由标准非线线拟合来模型化。本工作中,截止点动态地由最大化测量系数动态决定。每个测量中重新计算截止点,使得精度得以实现。现场应用中,这是优势。所以如果干扰条纹及时改变,算法会自动调整截止点 i0。
这些结果证明每一简单传感设置的性能(设置中有标准抗反射涂层和最小预防措施来最小化干扰条纹),可以利用提出的算法简单后处理数据得到较大改进。
本文,算法应用于Lorentzian线型(测量氧气浓度直接吸收光谱中的线型)。然而,算法能运用到别的线型,例如,一个沃伊特曲线,或带有不同函数形式的信号,源自,例如,从波长调制光谱。特别地,对于带有大振幅和半线宽度FSR的干扰条纹,它能很好地提取想要的信号, 对条纹和随时变化的条纹信号敏感。模拟数据初步的结果表明算法执行同样好的,如果信号振幅比条纹小10倍。进一步研究需要在相似的极端情况下测试算法性能。
综上所述,提出的算法,能从任意背景中提取信号特征,有干扰免疫 TDLAS的潜力,解决由背景随时变化带来的稳定问题,像热漂移。进一步讲,本算法不是特种的TDLAS,能应用到任何类型的光谱区,如果已知被检测信号的函数形状。
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
Acknowledgments
This work was carried out under a Commission for Technology and Innovation CTI grant (17176.1 PFNM-NM).
europepmc.org
europepmc.org
Abbreviations
The following abbreviations are used in this manuscript:
TDLAS Tunable Diode Laser Absorption Spectroscopy
FSR Free Spectral Range
CFT Continuous Fourier Transform
DFT Discrete Fourier Transform
RW Rectangular Window
HWHM Half Width at Half Maximum
VCSEL Vertical-cavity surface-emitting laser
Appendix A Approximation of the CFT by the Modified DFT
In this paper, the following definition for the continuous Fourier transform (CFT) is used
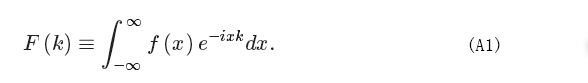
Let us first make some assumptions that will simplify the calculations. Let us assume that the function f(x) is zero outside a certain range (−a/2, a/2) with some a ∈ ℝ and a > 0 and let us indicate with m the number of data points at our disposal. For convenience, m is taken to be even. Let us introduce the sampling rate β as

The abscissas of the data xj and kj can be written as:


with j going from −m/2 to m/2. We can approximate Equation (A1) with a Riemann sum using the fact that f(x) is zero outside the range (−a/2, a/2):
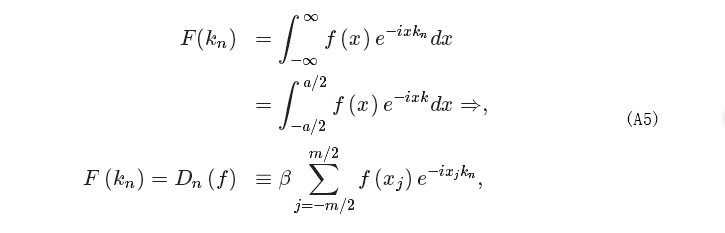
where we have approximated the integral with a discrete sum. Clearly, the bigger m is, the better will be the approximation. Now, using Equations (A3) and (A4), we can rewrite (A5) as
Author Contributions
F.V. conceived, designed and performed the experiments; U.M. proposed and developed the algorithm; F.V. and U.M. analyzed the data and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
1. Cassidy D.T., Reid J. Atmospheric pressure monitoring of trace gases using tunable diode lasers. Appl. Opt. 1982;21:1185–1190. doi: 10.1364/AO.21.001185.
2. Schiff H.I., Mackay G.I., Bechara J. The use of tunable diode laser absorption spectroscopy for atmospheric measurements. Res. Chem. Intermed. 1994;20:525–556. doi: 10.1163/156856794X00441.
3. Fehér M., Martin P.A. Tunable diode laser monitoring of atmospheric trace gas constituents. Spectrochim. Acta A. 1995;51:1579–1599. doi: 10.1016/0584-8539(95)01401-F.
4. Fried A., Henry B., Wert B., Sewell S., Drummond J.R. Laboratory, ground- based and airborne tunable diode laser systems performance characteristics and applications in atmospheric studies. Appl. Phys. B. 1998;67:317–330. doi: 10.1007/s003400050511.
5. Tuzson B., Henne S., Brunner D., Steinbacher M., Mohn J., Buchmann B., Emmenegger L. Continuous isotopic composition measurements of tropospheric CO2 at Jungfraujoch (3580 m a.s.l.), Switzerland: Real-time observation of regional pollution events. Atmos. Chem. Phys. 2011;11:1685–1696. doi: 10.5194/acp-11-1685-2011.
6. Nikodem M., Wysocki G. Chirped Laser Dispersion Spectroscopy for Remote Open-Path Trace-Gas Sensing. Sensors. 2012;12:16466–16481. doi: 10.3390/s121216466. [PMC free article]
7. McCurdy M.R., Bakhirkin Y., Wysocki G., Lewicki R., Tittel F.K. Recent advances of laser-spectroscopy based techniques for applications in breath analysis. J. Breath Res. 2007;1:014001. doi: 10.1088/1752-7155/1/1/014001.
8. Wang C., Sahay P. Breath Analysis using laser spectroscopic techniques: Breath biomarkers, spectral fingerprints, and detection limits. Sensors. 2009;9:8230–8262. doi: 10.3390/s91008230. [PMC free article]
9. Risby T.H., Tittel F.K. Current status of mid-infrared quantum and interband cascade lasers for clinical breath analysis. Opt. Eng. 2010;49:111123/1-24.
10. Curl R.F., Capasso F., Gmachl C., Kosterev A.A., McManus B., Lewicki R., Pusharsky M., Wysocki G., Tittel F.K. Quantum cascade lasers in chemical physics. Chem. Phys. Lett. 2010;487:1–20. doi: 10.1016/j.cplett.2009.12.073.
11. Linnerud I., Kaspersen P., Jaeger T. Gas monitoring in the process industry using diode laser spectroscopy. Appl. Phys. B. 1998;67:297–305. doi: 10.1007/s003400050509.
12. Lackner M. Tunable diode laser absorption spectroscopy (TDLAS) in the process industries—A review. Rev. Chem. Eng. 2007;23:65–147.
13. Kluczynski P., Jahjah M., Nähle L., Axner O., Belahsene S., Fischer M., Koeth J., Rouillard Y., Westberg J., Vicet A., et al. Detection of acetylene impurities in ethylene and polyethylene manufacturing processes using tunable diode laser spectroscopy in the 3-μm range. Appl. Phys. B. 2011;105:427–434. doi: 10.1007/s00340-011-4645-6.
14. Hodgkinson J., Tatam R.P. Optical gas sensing: A review. Meas. Sci. Technol. 2013;24 doi: 10.1088/0957-0233/24/1/012004.
15. Masiyano D., Hodgkinson J., Schilt S., Tatam R.P. Self-mixing interference effects in tunable diode laser absorption spectroscopy. Appl. Phys. B. 2009;96:863–874. doi: 10.1007/s00340-009-3690-x.
16. Hartmann A., Strzoda R., Schrobenhauser R., Weigel R. Ultra-compact TDLAS humidity measurement cell with advanced signal processing. Appl. Phys. B. 2014;115:263–268. doi: 10.1007/s00340-013-5599-7.
17. Werle P. Accuracy and precision of laser spectrometers for trace gas sensing in the presence of optical fringes and atmospheric turbulence. Appl. Phys. B. 2011;102:313–329. doi: 10.1007/s00340-010-4165-9.
18. Webster C. Brewster-plate spoiler: A novel method for reducing the amplitude of interference fringes that limit tunable-laser absorption sensitivities. J. Opt. Soc. Am. B. 1985;2:1464–1470. doi: 10.1364/JOSAB.2.001464.
19. Silver J.A., Stanton A.C. Optical interference fringe reduction in laser absorption experiments. Appl. Opt. 1988;27:1914–1916. doi: 10.1364/AO.27.001914.
20. Whittaker E.A., Gehrtz M., Bjorklund G. Residual amplitude modulation in laser electro-optic phase modulation. J. Opt. Soc. Am. B. 1985;2:1320–1326. doi: 10.1364/JOSAB.2.001320.
21. Sun H.C., Whittaker E.A. Novel etalon fringe rejection technique for laser absorption spectroscopy. Appl. Opt. 1992;31:4998–5002. doi: 10.1364/AO.31.004998.
22. Goldenstein C.S., Strand C.L., Schultz I.A., Sun K., Jeffries J.B., Hanson R.K. Fitting of calibration-free scanned-wavelength-modulation spectroscopy spectra for determination of gas properties and absorption lineshapes. Appl. Opt. 2014;53:356–367. doi: 10.1364/AO.53.000356.
23. Ehlers P., Johansson A.C., Silander I., Foltynowicz A., Axner O. Use of etalon-immune distances to reduce the influence of background signals in frequency-modulation spectroscopy and noise-immune cavity enhanced optical heterodyne molecular spectroscopy. J. Opt. Soc. Am. B. 2014;31:2934–2945. doi: 10.1364/JOSAB.31.002938.
24. Chen J., Hangauer A., Strzoda R., Amann M.C. Laser spectroscopic oxygen sensor using diffuse reflector based optical cell and advanced signal processing. Appl. Phys. B. 2010;100:417–425. doi: 10.1007/s00340-010-3956-3.
25. Li J., Yu B., Zhao W., Chen W. A review of signal enhancement and noise reduction techniques for tunable diode laser absorption spectroscopy. Appl. Spectrosc. Rev. 2014;49:666–691. doi: 10.1080/05704928.2014.903376.
26. Tenoudji F.C. Analog and Digital Signal Analysis. 1st ed. Springer International Publishing; Cham, Switzerland: 2016. pp. 111–113.
27. Tukey J.W. Spectral Analysis of Time Series. Wiley; New York, NY, USA: 1967. An introduction to the calculations of numerical spectrum analysis; pp. 25–46.
28. Harris F.J. On the use of Windows for Harmonic Analysis with the Discrete Fourier Transform. Proc. IEEE. 1978;66:51–83. doi: 10.1109/PROC.1978.10837.
29. Reid J., El-Sherbiny M., Garside B.K., Ballik E.A. Sensitivity limits of a tunable diode laser spectrometer, with application to the detection of NO(2) at the 100-ppt level. J. Appl. Opt. 1980;19:3349–3354. doi: 10.1364/AO.19.003349.
30. Tenoudji F.C. Analog and Digital Signal Analysis. 1st ed. Springer International Publishing; Cham, Switzerland: 2016. pp. 265–267.
31. Rothman L.S., Gordon I.E., Babikov Y., Barbe A., Chris Benner D., Bernath P.F., Birk M., Bizzocchi L., Boudon V., Brown L.R., et al. The HITRAN2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2013;130:4–50. doi: 10.1016/j.jqsrt.2013.07.002.
32. SpectraPlot the Wavelength Search Engine.
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
本文原著:Umberto Michelucci and Francesca Venturini
本文由山东如特安防设备有限公司LK编译,转载必须注明来自 sdrtkm.com
访问量:
此文关键词:干扰,干扰消除,噪声降低,数字滤波,光谱学,传感器